On schemes for learning to solve quadratic equations

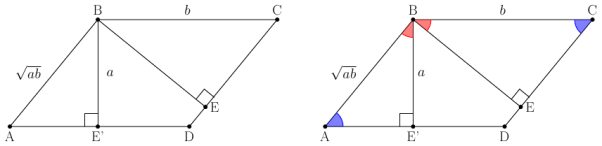
So I’ve recently been teaching the Math2c course at a swedish upper secodnary school and had some reasons to be thinking about quadratics because that’s like one third of the content of the course. Or well teaching is actually a bit charitable this time as the students at this particular school are among the most consistently diligent at self-study in the country that peppering them with instruction they’ve already read actually slows them down, but the role of instruction and individual work in learning mathematics at different levels is a discussion for another time.

So the model of teaching quadratics in most of the books I’ve seen typically runs something like this.

1. You start out some preliminaries about factoring techniques like the patterns and
2. You learn to solve the simplest quadratic by essentially explaining the pattern
3. You state the zero-product property (ZPP), that implies a = 0 or b = 0, and solve some quadratics that have already been factored like .
4. You learn the factoring method for solving quadratics without a constant term by factoring  and then applying the ZPP.
5. You (might) learn how to complete the square
6. You quickly use the method of completing the square to run though the proof of the pq-formula . (This does not use the ZPP nor the conjugate rule)
7. You spend a couple of hours drilling the aforementioned methods possibly.

Now functionally this route of progression definitely works for conveying how to solve these kinds of equations, but there are still some things I don’t quite like about it. First of all the methods reduce to three separate cases which superficially seem to have nothing to do with eachother

1. 
2. 
3. 

So whenever one solves a problem like this you first have to use identification of type, which is actually a lot harder to do than people who can already do it think it is. Also pedagogically the arrow of progression isn’t clear. Step 1 as presented has nothing to do with 2. The knowledge of step 3 is not used beyond step 4, and if the only use of completing the square initially is to prove the pq-formula the student will forget about this super important pattern and will have to relearn it at uni if ever.

I’ve thus been thinking if the scheme for learning how to work with quadratics might instead be replaced with:

1. Preliminaries on factoring, difference of squares, square of sum, distributive property.
2. Zero product rule and applying it to factored equations  (This should be complemented by graphing)
3. Solving by factoring with the difference of squares and applying the zero product rule. and and sneaking in problems the type
4. Solving by factoring with the distributive property
5. Learning to complete the square
6. Solving general quadratics by completing the square and then factoring with the conjugare rule
   
7. Derive the pq-formula from the factoring. (Now this is admitedly a lot messier than the normal way with )

Now there are many downsides to this scheme, for example step 3 being harder than the normal way on account of the normal way of applying operations to both sides is more analogous to solving linear equatons ,which is why it’s probably not used but it would be interesting to try it (or hear about if these is a book or school system) which approaches it this way. The final step 6, the method of factoring a general quadratic directly with the difference of squares is a technique which I find would be a useful addition to the scheme as I think it neatly exposes the connection between the three different forms in which you can write a quadratic expression in an algorithmic way instead of in a more formally logical way (invoking the general factor theorem).

Finally I’d just also like to summarize the method outlined in step 2 as a full algorithm because it more or less superceedes all of those messy “6-different ways, factoring by grouping methods” which I get when I google factoring.

Full algorithm for factoring a quadratic expression over the reals

1. Rearrange all the terms so that you have expression = zero
2. Complete the square of the expression (ignore if there is no linear term)
3. Rewrite the constant term as a square (possibly by)
4. Apply the conjugate rule to the difference of two squares

The 7 Tetris block circumference problem

Fancified name in the title aside I was checking out some worksheets for geogebra yesterday and came across one which had predefined tetris block elements. I played around building different shapes, originally wondering if you could make a periodic pattern out of an even ditribution of tetris blocks but I eventually landed on a different question which will be the topic of this prost.

So you start with the 7 basic tetris blocks as featured in the image below.So these pieces you can stick together into chunks in an amazing number of ways and each new figure naturally has some circumference. Assuming all the pieces fit rogether in one chunk the maximal circumference such a figure can have is 56 (think about it) but the question quickly becomes: What is the least circumference such a composite piece can have?

Here are some of the initial trial and error solutions which I played around with

but there nevertheless is a packing with even smaller circumference and it is proving the existence and minimality of this packing that will be the theme of this post.

The connection between diameter and pi

So I was having the worst headache and lying in bed thinking about simple geometry problems waiting for the pain killer to kick in. One of the things I did was compute the perimeter/circumference of the Reuleaux triangle. Okay so that one’s parameter is composed of three sixths of a circle with radius twice the widthof the triangle so if the width of the triangle is that’s . Similarly for all the other Reuleaux polygons the ()-sided reuleaux polygon . Huh… I thought. That’s kind of odd. All of these figures with constant widths have the same circumference formulas as the circle which of course has constant width called the diameter.

And looking up the wiki-article on shapes of constant widths and this is apparently a thing proven in 1860. All curves with constant width have a perimeters which is times it’s width. and it’s called Barbier’s theorem.

I also get the feeling that this should be possible to be reworked into a pro-pi argument in the tau-vs-pi debate. Of course by the law of the equivalence between pi and tau implies it could be made into a pro-tau-argument as well but since I’ve never seen it come up in one of those debates I would like to see what happens when a tauist brings up that defining the circle constant via the diameter of a circle was a mistake since the radius is a more fundamental property and then have the piist counter that at least there is a whole class of objects with diameters and they all have perimeters which are  times the diameter : P

Folding polyhedra and a novel connection between folding a tetrahedron and a 2D result.

So I’ve been folding a lot of polyhedrons out of paper this past week. Like a lot… But since the types of interesting polyhedrons I have left to built take a bit too long to construct adn I already wasted enough time folding the (small) stellated dodecahedron.

Instead I’m rather reviewing the ‘legitimacy’ of the folding schemes and figure out what relations actually govern weather something fits together or not. The prototypical example is the tetrahedron, the polyhedron with the fewest number of faces. The explicit construction of the regular tetrahedron (all sides equilateral triangles) is easy to show directly and is found in the elements and elsewhere but you can fold generic tetrahedrons by just making 4 triangles such that every triangles has common sides with the other triangles in a natural way. Made from one piece they are then flded together to form a possibly irregular tetrahedron. 

Empirically and intuitively this basically defines natural, a result in no need of further explanation. Nevertheless mathematically it almost seems coincidental. Just because two face can be glued pairwise doesn’t immediately mean all the faces should fit together collectively even though it’s about as natural a thing to postulate as the equality of the two base angles in an isosceles triangle.

The novel thing is that you can turn this 3 dimensional problem into a 2 dimensional one and use the vast machinery available to you in that space. You can note that folding an individual side is equivalent to rotating it about it’s common side with the bottom triangle where the it’s outer corner traces out a circle lying in a plane parallel to the altitude of the triangle and perpendicular to the common side.

If the three faces are to come together their corresponding circles must intersect at a single point which means 1. the planes of rotation intersect along a common line (which is perpendicular to the plane and forms the height of the tetrahedron and 2. with the altitudes of the faces and satisfying relations to guarantee a consistent height.

Especially 1. is interesting because it forms a more ‘physical explanation’ for why dropping and extending altitudes in the original net intersect at a common point which can be taken as a purely classical 2 dimensional geometric result.

The thing I find neat is that this result seems kind of arbitrary in 2D but as part as a 3-dimensional picture it makes perfect sense.

I’ll have to see what’s the best way of extending this to folding schemes with a general polygonal base.

The cuboid volume formula and the dissection of a cuboid into a cube

So at the end of the last post I gave the outline of the idea of how you might extend the dissection of a rectangle into a square and the definition of area to an analogous procedure for the cuboid and it’s volume. The idea is really simple but I thought I’d practice my diagram writing skill by providing an illustration and expand the definition of volume.

Okay so we say that we have a cuboid with dimensions where we conventionally say that it has volume meaning it has the same volume as a cube with side . Let us use dissection to motivate this; that is describe a procedure of cutting up the cuboid and reassembling it into the prescribed cube.

We will essentially perform regular rectangle to square dissections face-wise splitting the cuboid into prism.

Let us start with the face and dissect it into a rectangle having one side and the other (by the area formula) being .Applying this to the whole cube the cuts through the face are extended through the solid along planes perpendicular to the face forming prism which are rearranged to form a new cuboid with as one of it’s side.

Note the depth of the cuboid is unaffected by this procedure.

(You might need more pieces than the image indicates)

Next we turn out attention to the face with sides and and perform the same procedure where this face is transformed into a rectangle with one side being by construction and the other side

And so this face is square! All the sides of this cuboid are therefore equal and we’ve ended up with a cube.

*This procedure is not original but my interpretation hasn’t been checked so some caution should be taken

Sidenote: Just as triangles and polygons can be dissected to rectangles a prism can therefore be disected into a cube as well and paying attention to the details of such a procedure you recover the conventional formula for general prism. For the cylinder we don’t have any elementary means of dissecting into a cube but just as you may approximate a cirvle by triangles you can approximate the cylinder by triangular prisms and obtain the standard formula.

Dissection of a rectangle into a square and a definition of area

This post is simply a reworking of my previous post on this subject as I realized I had missed a special case which is accounted for in a single line but which nevertheless had gone unmentioned. The problem was to start with a rectangle of dimensions , naturally having area and cutting it apart into pieces which are then rearranged to form a square with the same area.

This procedure involves abusing the knowledge that the resulting square will have as the lengths of its sides where you start by cutting a ‘pseudo-diagonal’ having this length across the rectangle, having sliced of a triangular corner. Displacing this corner to the other side of the rectangle you obtain a parallelogram with as its base and implicitly also as its height by virtue of the known area. This parallellogram is then cut along on of it’s altitudes normal to the side with length and rearranging this pieve the resulting shape is a square. Diagrammatically the procedure is shown below.

Note 1: There were two things I wanted to expand on regarding this procedure. Firstly that it needs to be supplied an additional step if the rectangle is too wide. More precisely if the base is more than twice the height. If that is the case an additional cut will be required. We may first note the limiting case where the second cut now  intersects with one of the corners

and if the width is increased beyond this limit our desired seond piece is only partially contained in the actual paralellogram. You see pretty much immediately that all you need is to move this piece and then slice of a tip segment and move that but it’s nevertheless an additional step which should have been noted upon.

Note 2: The second thing I wished to expand upon was simply argument for the fact that this actually forms a square. Knowing all the formulas for area it is pretty easy to fill in all the blanks such as that parallelogram with area and and base must have height $a$ or if a rectangle has area and base $b$ then its height would be and so on.

However it would be much neater to take this rearrangement as the proof that the area of a recangle with sides $a\times b$ has area . To outline this proof I will make use of this particular definition of area:

If a geometrical figure can be cut into a finite number of smaller pieces and rearranged into the shape of a square with side we say that the figure has area . 

This is not a complete definition of area as what constitutes a ‘piece’ and ‘rearranged’ is unclear and not all figures are necessarily rearrangeable and like all casual definitions it might invite paradoxes but it allows us to form a class of figures which we say have equal area and make more practical sense of that means instead of just memorizing formulas. For example to say an A4 paper has an area of 623.7 cm^2 now means it can be cut and rearranged into a square with a $\sqrt{623.6} = 27.97$ cm side.

The part of the dissection which I would like to prove without references to area that the resulting shape really is a square. With reference to the diagram below we say we have a parallelogram height and base so such that it’s slanted side has length and wish to show that the altitude normal to DC goign through B, BE, also is

This is most easily proven using the similarity of the two triangles AEB and EDB which follows from the angles A and C in a paralellogram being equal. From this we get

and thus

Therefore it is truly a square that the rectangle is being rearranged into and just to be needlessly pedatic lets once again note that all this meant that a rectangle with dimensions was possible to rearrange into a square with side meaning the area of the rectangle really is !

Sidenote: What jogged my memory on was that I’ve been thumbing through this Peter R: Cromwells rather charming book Polyhedra where the problem of how you might define volume partially (but ultimately not exclusively) though dissection sprang to mind. On page 45 I also recovered another outline of how to dissect a general polygon to a square though with a different final step than my own and for whatever reason omitting the step outline above. In principle you should be able to perform this dissection ‘face wise’ to prove the volume formula of a prism (or rather the cuboid) but I’ve yet to complete the details of the proof.

You see with only four colors you may… Oh wait what?

Earlier today a guy sitting next to me was just killing time by just drawing random figures in MS Paint and using the fill in areas with the fill in tool. I was going to humor him to try to color his picture with as few colors as possible (with the rule that no adjacent zones have the same color). I was presuming that we would end up with something hinting at the 4-color theorem but as I was doodeling I began to realize that there was something weird going on. You see… I only seem to need 2 colors to color my partitions of the plane. The actual partition is created by tracing a continuous line around and only allowing pair-wise intersections and eventually closing it on itself.

I

After some inspection I’ve come to the conclusion that whatever is going on is a consequence of the way I am tracing out the curve, where the fact that I am not allowing  the line to pass though the same point more than twice so every vertex in the corresponding graph always has 4 neighbors which must be the source of it.

Could of course also just be an odd coincidence that my partitions have had this property but I am nevertheless looking forward to figuring out why or how to construct a counterexample.

EDIT: July 2015. Since as it stand I’m probably not making another post on this until I’ve come up with an original proof I’d nevertheless like to add that the result indeed holds and is exclusive dependent on every vertex having even degree (in this case). “The two color theorem” will produce some proofs but if you have Peter Cromwells Polyhedra available at your local library I’d like to recommend it’s chapter on colorings which contains a proof of a slight rephrasing of this result on page 339-341 on top of some other novel results.

Spending the weekend folding polyhedra and finding convex internal angles

So I’ve managed to resolve the circle construction question from a few posts back and determined that any number n can be constructed by a fairly small number of operations; more precisely the 2-logarithm the number but I’ve put off putting together a good description of the proof as I’ve been preoccupied with school, work, and another new mini-project: Polyhedra.

I originally got the idea that I should look back into Polyhedra after I overheard some students mentioning the concept of the Euler characteristic of a graph (V + F – E) and recognizing that I remembered very little of that particular theory I set to refreshing on the theory and making lots of paper polyhedra, drawing Hamiltonian paths, and colorings and so on as I stumbled over them.

As I reviewed the E + F – E = 2 proofs I also had to recognize that I had some gaps in my knowledge regarding the formal existence of triangulation of polygons and continued on the merry chain of ‘better check that’ untill I at the bottom of the chain ended up with

Every polygon has a strictly convex angle. (An internal angle less than )

A statement for which I designed the following proof (which I unfortunately realized had some issues as I was typing it)

Let   be the polygon spanned by the points in the plane. Consider the line formed by extending the segment and let be a vertex on $P$ which is of maximal distance from $L$. Or more precisely has the following property

• For any other vertex on the distance from to the line is shorter or equal to the distance between and $L$.

Now (using the Paralell postulate) let be a line through which is parallel to . By construction all vertices on either lie on or on the same side of as ( and ). Let us for convenience say that lies on the ‘south side’ of .

At most one of s neighbors in the polygon on lie on  (for otherwise it would be a redundant vertex) and so the angle formed by these three points contained on the south side of $L’$ is strictly convex and it is an internal angle of . (It is internal for a ray from due north into intersects the polygon 0 times (an even number). We have therefore found a strictly convex internal angle!

I will have to admit that I realized an issue with this proof as I finished it as I had somewhat embarrasingly not properly considered how to formulate (prove) that the ‘south’ angle at was indeed the internal one and it sort of exposes that I haven’t collected enough formal devices to differentiate between angles of the form and $latex EDC without coordinates or images and the proof isn’t as satisfactory as I’d like and I will see if I can fix it.

The image I had in my mind for why this was true was after all pretty straight forward.

Using higher maths the existence of a strictly convex internal angle can be straightforwardly deduced from the existence of the convex hull as the convex angles of the hull put upper bounds on at least 3 internal angles of any polygon. But it of course has the issue of just kicking the ball further down the corridor as you’d have to prove the existence of a convex hull.

Constructions with a compass alone

Back Tuesday I discovered the rather tantalizing Mohr-Masceronic theorem which essentially says that anything you can do with a compass and straight edge you can do with a fixable alone. It’s not exactly that the straight edge is completely redundant …

Constructing more integers using compass. 7 and 15.

Tired an a little bit hungover today I decided to play some more with the concept of constructing a multiple lengths with a compass and as few operations as possible; the problem I sketched yesterday in: https://seriouscephalopod.wordpress.com/2015/04/03/o/

Nothing interesting really except firstly I realized I had missed that there was a 3-circle construction of ‘7’ while I had originally displayed a 4-circle construction in the original post and I suppose I should correct myself plus I thought it was kind of cute.

Besides for that i suppose I have tried to gather some more empirical data regardning these constructions. I tried to write a program to runt through all simpler construction as if in a tree diagram with a new node added in every step but not having figured out a good cutoff condition I got stuck with too many ‘stupid constructions’ since I counted them all and the data set grew to quickly in relation to the data I got so I decided to scrap the algorithmic approach before I’ve figured the system better.

So I just tried to find constructions by hand and though my ‘minimas’ are only upper limits than unquestionable minimas as a result but here are the first minimal construction numbers which feel somewhat certain at least.

2	1
3	2
4	2
5	3
6	3
7	3
8	3
9	4
10	4
11	4
12	4
13	4
14	4
15	4
16	4
17	5

At least in the beginning it has turned out that the powers of 2: 4,8,16 have formed good proto-constructions from which I can add just one circle to get to a nearby number so you can see that the number of circles necessary increases as you pass 4, 8, and 16. This might just be a quirk of the fact that these numbers are still pretty close to eachother or it is something fundamental. Nevertheless I can as the following question for further inquiry:

Question 2:  For some is there a number such that such that the minimal number of circles necessary to construct is less than ()?

I suspect there is but we’ll see… I was however able to find a counterexample to Question 1 in the previous post.

Question 1:  Is the inequality

in fact an equality or what is the smallest  such that it is a strict inequality?

That is as there better constructions than just reusing the constructions for it’s factors. The counterexample I found was 15 = 3 * 5 which using first the 3-step construction for 5 and then multiplying that by 3 using 2-circles takes a total of 5 circles as seen below

Red circles first construct 5 and blue circles then construct 15 from multiplying 5 by 3.

However using first the 3-step construction of 8 and then adding one more circle you can get to 15. 

So the inequality was not an equality. That’s nice because on one hand it would have been a scarily powerful result had it been true but this way (it being not) I don’t have to think about it anymore.